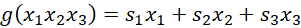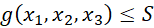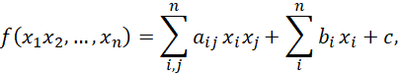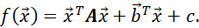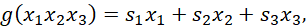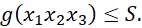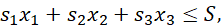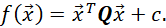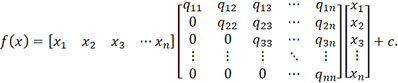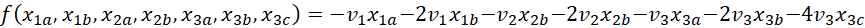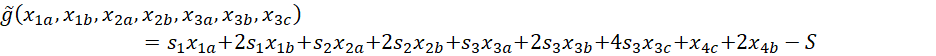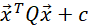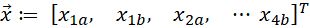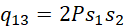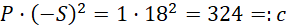- SAP Community
- Products and Technology
- Technology
- Technology Blogs by SAP
- AN INTRODUCTION TO QUADRATIC UNCONSTRAINED BINARY ...
- Subscribe to RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Report Inappropriate Content
Navigating Optimal Solutions: An Introduction to Quadratic Unconstrained Binary Optimization (QUBO)
In the landscape of decision making and problem solving, optimization stands out as a path to efficiency and excellence for enterprise. Optimization seeks to find the most favourable outcome from a multitude of possibilities, providing solutions that are not only effective, but often transformative.
For many optimization problems to run on quantum hardware or quantum-inspired hardware, (see our earlier blog here), they must be converted into a QUBO, a mathematical framework uniquely tailored to tackle problems characterized by many discrete, binary choices. Whether optimizing resource allocation in complex logistics networks, fine-tuning parameters in machine learning algorithms, or solving combinatorial puzzles in artificial intelligence, QUBO proves to be a versatile and powerful tool.
In this blog, we explain some of the mathematical principles that underpin QUBO problems. As we navigate this mathematical landscape, we will see how optimization guided by QUBOs becomes not just a theoretical construct, but a tangible force that shapes and refines solutions to some of the most complex problems.
Optimization Problems
Optimization problems lie at the heart of numerous disciplines, serving as a fundamental concept in mathematics, engineering, computer science, economics, and beyond. These problems revolve around finding the best possible solution from a set of feasible alternatives, often aiming to maximize or minimize a certain objective function under given constraints. Whether it's finding the most efficient route for a delivery truck, optimizing resource allocation in a manufacturing process, or fine-tuning parameters in machine learning algorithms, optimization is a pervasive and indispensable tool for solving problems in diverse fields. The complexity and real-world applicability of optimization challenges have led to the development of various algorithms and methodologies, making it a rich and dynamic area of study with far-reaching implications.
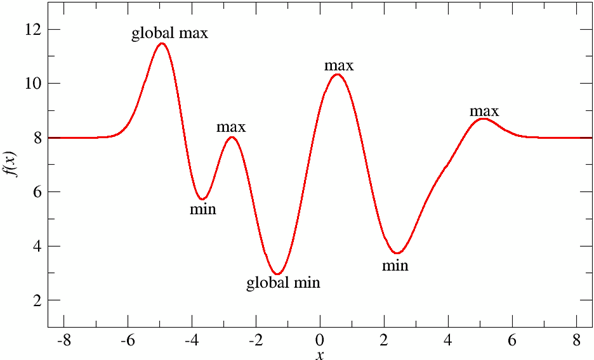
Figure 1, below, illustrates the essence of optimization problems using a 1-D graph with both local minima and a singular global minimum. In this visual representation, the x-axis represents the feasible solution space, while the y-axis represents the objective function value. The graph visually captures the inherent challenge of optimization: determining the input that yields the smallest (or sometimes largest) value of the objective function while navigating through various local optima.
A 1-D Cost Function
Figure 1: Here, we can see a cost function (in this case a 1-D function) with the global minimum at x=-1.5 and several local minima. If we were to use classical methods to find the global minimum, the likelihood of getting stuck in a local minimum is great.
The Knapsack Problem
To truly understand optimization problems, it’s worth looking at something of a textbook optimization example: the knapsack problem.
Imagine a scenario where you have some goods to trade at a nearby market, you must decide what items to bring in your knapsack, and to maximise your profits you want to carry as much value as possible. This knapsack has a maximum capacity (dictated either by its size or perhaps by how much weight you can carry). In our example, the knapsack has a maximum capacity (how much you can carry) of 18 (we’ve chosen a unitless value here, but you’re free to choose whatever you like.)
Item | Size (s) | Value (v) |
Potato chips (crisps) | 7 | €4,55 |
Packet of biscuits | 5 | €3,20 |
Apples | 3 | €1,80 |
Table 1: The options of provisions to carry in your knapsack with their sizes and values.
In the knapsack problem, we want to maximize the monetary value of the items in our knapsack. This is similar enough to minimization that we only need to mention that it involves a change of sign.
With this information we can start modelling our problem. To do this we need to define; variables, which describe what we can change; parameters, which describe what we cannot change; an objective function, which outputs a value based on a particular variable configuration; and finally, a list of constraints, which are equalities or inequalities that must hold.
For example,
- Variables x₁, x₂, x₃,... The quantity of each item
- Parameters s₁, s₂,... The size of each item
- Objective function f(x₁, x₂, ... xₙ) Total value in the knapsack’s contents
- Constraints g(x₁, x₂, ... xₙ) Total size of the items, cannot exceed S = 18
In this case, the quantities of chips, biscuits and apples are denoted by x₁, x₂, and xₙ
The corresponding values (prices), and v₁, v₂, and v₃. are taken from Table 1 (above). The objective function is then,
This is subject to the constraint,
where sᵢ are integers and represent the size of each corresponding item and S = 18. We will also restrict our boxes, bags and apples to positive integer values. After all, it makes no sense in this context to carry around negative apples.
With our problem mathematically defined, all that remains is to solve it. There are current algorithms that are designed to do this, some of them quite good, depending on the problem. Perhaps we just want a number that’s close enough, and we’re not interested in the absolute minimum.
So, we need to turn to new paradigms. To solve this on the digital annealer, we need to take a few steps and convert it to a QUBO. Let’s delve a little deeper into what the letters in this abbreviation stand for.
1. Quadratic
You may remember this from your first algebra classes. Quadratic simply means squared, but it also means that you can multiply two different variables, but not three or more. So x is allowed, as well as xy and x², but not x³ or x⁴, nor any terms with larger exponents. For our optimization to work, no terms higher than quadratic are allowed. We can write the general form of our quadratic like this,
where c is a constant. If we consider xᵢ and bᵢ as a list of numbers (or vectors), we can consider aᵢⱼ as a table (or matrix), we can rewrite the general form in matrix-vector form,
2. Unconstrained
Didn’t we just talk about how constrained the whole problem is? Well, yes, but there’s a way around that. What if, instead of constraints, we could introduce a penalty function what serves to steer us away from values that violate the constraints? A penalty function allows the cost function to exist at points where constraints would prohibit it, with the caveat that it raises the cost to something prohibitive. Penalty functions differ with each problem (as do constraints). So we will limit ourselves to the problem at hand, remembering our constraint,
The trick is to introduce auxiliary variables (sometimes called ancilla or slack bits).
with x₄ ≤ 0
We now need to add this penalty, g, to our cost function, f, and scale it by a penalty factor, P and square the function g so it will never be negative.
The penalty factor P tells us something about how much the above cost function, which we can abbreviate as f(x)+Pg(x)², is punished if a solution is invalid. If P is too large: The barriers between the local and global minima become prohibitively high; limiting our ability to leave a local minimum and find a global one. If the penalty factor is too low: An invalid solution may have a lower value than the global minimum that we are looking for.
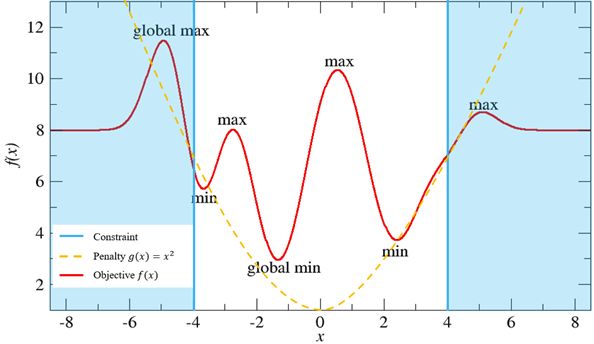
Figure 2 below is an example of both constraints and a suggestion for a penalty function that might work with such constraints. All that remains is to add the squared constraint to the cost function and scale it appropriately.
A 1-D Cost Functions with constraint and penalties
Figure 2: The constraints in the above plot prohibit the x-axis from taking values less than -4 and greater than 4. As a QUBO must be unconstrained, we have included an x² term that can be scaled appropriately and then added to the objective function.
3. Binary
So far we have been thinking and working with integer numbers. But quantum computers cannot solve these as they are, they must be converted to a binary problem, x⋲ {0,1}. (The variables can only be either 0 or 1). If you’re familiar with computer science, you’ve probably come across binary numbers before, so this blog won’t go into detail. It suffices to mention that it does provide a useful trick for simplifying some of our expressions, as squaring a binary number leaves it unchanged, xᵢ² = xᵢ. This allows us to rewrite our general matrix vector form above as
with Q as an upper-triangular matrix and c as a constant.
4. Optimization
More explicitly, we can rewrite our vector equation in its component form, with qᵢⱼ as the components of the upper-triangular (or symmetric) matrix that contain information about our problem. And xᵢ as the binary values indicating whether we want to include an item (or combinations of items). Expanding the previous equation gives,
The size of our vector x̅ depends on the problem. In the case above, we do not want to restrict it to one of each item. To expand our options, we can “itemize" some of the possible combinations.
As a final “trick”, we can add air as an item to insert our slack items mentioned above. Our table then becomes Table 2 (below).
Item | size (s) | Value (v) |
One packet of chips | 7 | €4,55 |
One packet of biscuits | 5 | €3,20 |
One apple | 3 | €1,80 |
Two bags of potato chips | 14 | €10,10 |
Two packets of biscuits | 10 | €6,40 |
Two apples | 6 | €3,60 |
Four apples | 12 | €7,20 |
One unit of air | 1 | €0,00 |
Two units of air | 2 | € 0,00 |
Table 2: Our new table of items to account for binary vectors and multiple items of the same type. Different quantities of air are included as an ancilla to account for constraints.
Take the Red Pill
We’re now (finally) ready to reformulate our QUBO. From the table above, we can build the matrix Q. In binary form, our QUBO can be stated as minimizing,
Where:
with,
And S = 18 subject to xᵢ⋲ {0,1} and in this case we will let P = €1,00. As indicated earlier, we can equivalently formulate the minimization problem in terms of a coefficient matrix and binary decision variables in a vector notation:
minimize
for
Then, the coefficient in Q corresponding to the product x₁ₐx₂ₐ arises from the term
and evaluates to
Similarly, when squaring g, we get a constant offset
Now we have all the terms of our optimization problem. We can input this matrix and constant term into our optimizer to allow it to return the vector x. Remember, this will be a string of ones and zeros corresponding to inclusion or exclusion of the items in table 2.
Why?
The knapsack problem is just an illustration. Nearly all enterprises have problems that require some form of optimization, because what is a business if not a system that seeks to maximize profit given a choice of markets.
Having established the basic framework of the QUBO approach, we encourage you to explore its applications by visiting the blog article on SAP's proof of concept (PoC). In the PoC, we ran tests pitting Fujitsu’s Digital Annealer Unit against classical optimizers to assess performance and accuracy. While no formal training in QUBO problems is required to read the blog, we thought a primer for the reader might help to provide relevant context.
Acknowledgements: Peter Limacher for his work creating the QUBO example and illustrations for SAP's quantum eXplorers' bootQamp 2023.
You must be a registered user to add a comment. If you've already registered, sign in. Otherwise, register and sign in.
-
ABAP CDS Views - CDC (Change Data Capture)
2 -
AI
1 -
Analyze Workload Data
1 -
BTP
1 -
Business and IT Integration
2 -
Business application stu
1 -
Business Technology Platform
1 -
Business Trends
1,658 -
Business Trends
93 -
CAP
1 -
cf
1 -
Cloud Foundry
1 -
Confluent
1 -
Customer COE Basics and Fundamentals
1 -
Customer COE Latest and Greatest
3 -
Customer Data Browser app
1 -
Data Analysis Tool
1 -
data migration
1 -
data transfer
1 -
Datasphere
2 -
Event Information
1,400 -
Event Information
67 -
Expert
1 -
Expert Insights
177 -
Expert Insights
301 -
General
1 -
Google cloud
1 -
Google Next'24
1 -
GraphQL
1 -
Kafka
1 -
Life at SAP
780 -
Life at SAP
13 -
Migrate your Data App
1 -
MTA
1 -
Network Performance Analysis
1 -
NodeJS
1 -
PDF
1 -
POC
1 -
Product Updates
4,577 -
Product Updates
346 -
Replication Flow
1 -
REST API
1 -
RisewithSAP
1 -
SAP BTP
1 -
SAP BTP Cloud Foundry
1 -
SAP Cloud ALM
1 -
SAP Cloud Application Programming Model
1 -
SAP Datasphere
2 -
SAP S4HANA Cloud
1 -
SAP S4HANA Migration Cockpit
1 -
Technology Updates
6,873 -
Technology Updates
429 -
Workload Fluctuations
1
- External System Integration in DMC in Technology Blogs by Members
- Unveiling Customer Needs: SAP Signavio Community supporting our customer`s adoption in Technology Blogs by SAP
- Exploring SAP Cloud ALM and its functionalities in Technology Blogs by Members
- Workload Analysis for HANA Platform Series - 2. Analyze the CPU, Threads and Numa Utilizations in Technology Blogs by SAP
- SAP PI/PO migration? Why you should move to the Cloud with SAP Integration Suite! in Technology Blogs by SAP
| User | Count |
|---|---|
| 32 | |
| 17 | |
| 15 | |
| 14 | |
| 11 | |
| 9 | |
| 8 | |
| 8 | |
| 8 | |
| 7 |